Equilibre d’un poids suspendue en un point quelconque d’une chaîne tenue en deux points

Comment exprimer l’équilibre d’un poids agissant en un point quelconque d’une chaîne ?

Si nous considérons maintenant le cas où le poids n’est pas placé au milieu de la chaîne, mais plus près du support de droite, il est toujours possible de résoudre graphiquement le système, mais cette fois-ci les efforts dans les deux tronçons du câble ne sont plus égaux. On constate que la partie de la chaîne qui relie le poids à l’appui le plus proche prend une part substantiellement plus grande que celle qui le relie à l’appui le plus éloigné.

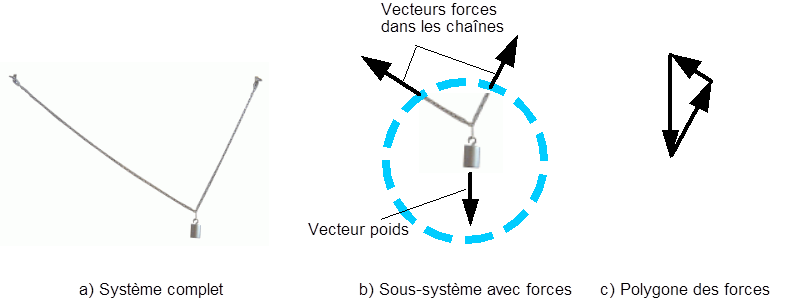Figure 4: Chaîne avec un poids suspendu de manière asymétrique

On constate qu’il existe une relation de triangles semblables entre l’image de la chaîne avec son poids et le diagramme des forces.

Un petit complément : pour qu’un corps soit en équilibre, il ne suffit pas que la somme vectorielle des forces qui agissent sur lui soit nulle, même si c’est une condition nécessaire.
Il faut aussi que les trois forces soient concourantes en un point, comme on le voit dans la figure 4b) ci-dessus.