Equilibre d’un poids suspendu à une chaîne

Comment exprimer l’équilibre d’un poids suspendu à une chaîne ?

Prenons l’exemple d’un corps de masse M suspendue à une chaîne (fig. 2). Sur cette masse agit l’attraction terrestre g ce qui conduit à une force de poids P = M · g agissant en direction du centre de la terre, ou plus simplement verticalement vers le bas. Si nous isolons mentalement un système (que nous appelons sous-système) comprenant la masse et un petit bout de la chaîne, on constate que pour que ce sous-système soit en équilibre, il est nécessaire que la force présente dans la chaîne soit égale et opposée au poids suspendu (en négligeant le poids de la chaîne elle-même). La somme vectorielle des forces agissant sur le sous-système est nulle, donc le sous-système est en équilibre.

C’est ce que montre le polygone des forces, dans lequel les forces ne sont pas nécessairement dessinées à la même échelle que dans le dessin du sous-système. Il est à noter que dans le polygone des forces les deux forces devraient être effectivement superposées l’une sur l’autre ; elles ont été dessinées avec un petit espace entre elles pour faciliter la compréhension.

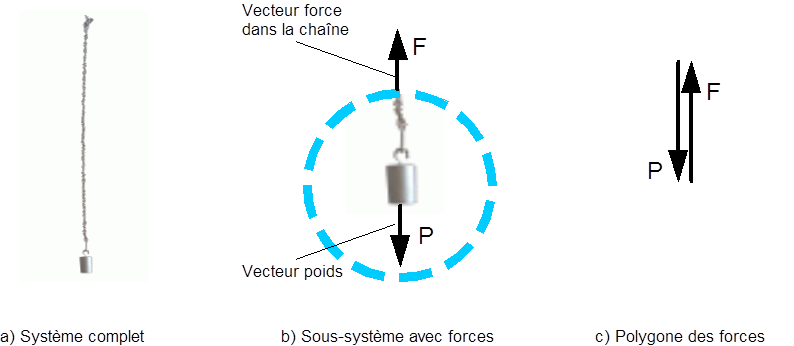Figure 2: Poids suspendu à une chaîne