Equilibre d’un poids suspendu au milieu d’une chaîne tenue en deux points

Comment exprimer l’équilibre d’un poids agissant au milieu d’une chaîne ?

Considérons maintenant le cas un peu plus compliqué d’un poids agissant sur une chaîne tenue à deux appuis. Sous l’action du poids, la chaîne se tend. Considérons de nouveau un sous-système incluant le poids en deux petits bouts des deux tronçons du câble qui le supportent. Pour ce que sous-système soit en équilibre (et nous savons qu’il l’est, puisque la photo le démontre !), il faut de nouveau que la somme vectorielle du poids et des deux forces dans les deux tronçons du câble soit nulle. On constate qu’il est possible d’obtenir graphiquement la solution de ce problème en dessinant le polygone des forces agissant sur le sous-système : d’une part le poids et d’autre part les deux forces des deux tronçons de la chaîne.

Encore une fois, pour que le sous-système soit en équilibre, il faut que la somme vectorielle des forces agissant sur lui soit nulle, ce qui peut aussi se formuler comme l’exigence que le polygone des forces soit une figure fermée (un polygone et non une ligne polygonale). Dans le cas présent, la charge agissant au milieu de la chaîne, il n’est pas très surprenant que la force dans les deux tronçons du câble soit la même.

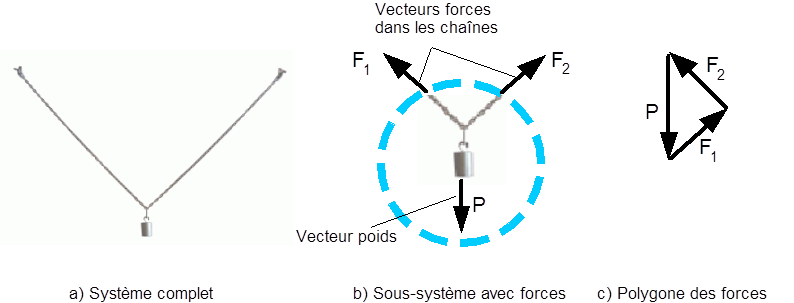Figure 3: Chaîne avec un poids suspendu en son milieu

Si on dessine le polygone des forces à une échelle connue (10 cm pour 10 N p. ex.), on peut lire à la même échelle la valeur de la force dans les deux tronçons du câble. C’est sur ce principe qu’a été développée la statique graphique qui a été utilisée au XIX^è et au début du XX^è siècle pour le calcul des constructions. Pensez par exemple à la Tour Eiffel à Paris, à l’époque il n’y avait pas d’ordinateurs !