Dans la première partie du cours, les structures étudiées étaient de formes funiculaires. Leur forme est déterminée sur la base du polygone funiculaire des charges appliquées. Dans les leçons relatives au thème des arcs, nous avons vu que la forme idéale d’un arc correspond au polygone funiculaire des charges principales.

Le problème de la stabilité des arcs en maçonnerie en présence de charges variables a été mis en évidence, en arrivant à la conclusion qu’un arc en maçonnerie peut devenir instable, se transformant en un mécanisme de barres articulées entre elles. Ces articulations apparaissent lorsque la ligne d’action de l’effort atteint un bord extrême de l’arc.

Si par contre l’arc est réalisé avec un matériau qui, en plus d’avoir une résistance à la compression, a également une résistance à la traction, il est alors possible que la ligne d’action de l’effort sorte de la section sans que cela ne conduise à l’instabilité du système.

C’est pourquoi les matériaux qui ont une résistance à traction et à la compression, comme l’acier, le bois ou le béton armé, offrent une plus grande liberté dans le choix de la forme de la structure, en permettant de réaliser des “arcs” avec une forme non funiculaire. De telles structures sont appelées cadres : l’image ci-dessous nous montre un exemple de cadre en bois qui soutient la toiture d’une salle polyvalente.

Salle polyvalente à Bad Ragaz (Saint-Gall), arch. Broder et Hug, ing. Hans Werner, 1979

Le choix de réaliser un cadre plutôt qu’un arc est dans la plupart des cas dicté par des exigences fonctionnelles, liées à l’utilisation de l’espace utile de la construction ; c’est par exemple le cas de l’exemple ci-dessous.

Sous-sol de la “Caserma di Tommaso”, Rome, ing. R. Morandi, 1951

La leçon qui suit présente l’analyse structurale des cadres en cherchant avant tout de comprendre l’influence de l’excentricité du polygone funiculaire par rapport à l’axe de la structure en termes d’efforts internes. Le pas suivant sera l’explication du fonctionnement structural des cadres au moyen de modèles inscrits à l’intérieur du matériau, comme illustré ci-dessous.

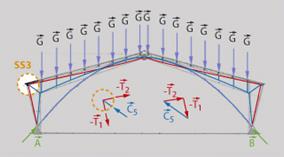Modèle structural pour un cadre

Nous étendrons ensuite les analyses au cas des cadres avec porte-à-faux, en analysant l'influence des porte-à-faux sur les efforts dans la structure et en traitant le problème de la détermination des efforts à l'intérieur des éléments d'un modèle structural inscrit dans le matériau.

Halle de sport “Buchholz” à Uster, arch. C. Gröfensteiner, S. Camenzind, 1998